國立清華大學開放式課程
A-
A
A+
03-5715131#35401
mengfen@mx.nthu.edu.tw 吳小姐
繁體中文
简体中文
English
網站說明
About
網站簡介
授權合作
榮譽事蹟
平台操作
服務項目
最新消息
News
最新上傳
最新公告
開放課程
Open Course
新增課程
所有課程
工程學群
自然科學學群
人文社會學群
熱門教材
Popular Textbook
工程學群
自然科學學群
人文社會學群
專欄報導
學生筆記
師資團隊
Teachers
清華講座
NTHU Lecture
全英語課程
EMI
全英語課程
YT熱門影片
相關資源
Discussion
學術
網路自學
ADOBE專區
教學專區
平面設計
進階搜尋
國立清華大學開放式課程
網站說明
網站簡介
授權合作
榮譽事蹟
平台操作
服務項目
最新消息
最新上傳
最新公告
開放課程
新增課程
所有課程
工程學群
自然科學學群
人文社會學群
熱門教材
工程學群
自然科學學群
人文社會學群
專欄報導
學生筆記
師資團隊
課程討論
工程學群
自然科學學群
人文社會學群
清華講座
全英語課程
相關資源
學術
網路自學
ADOBE專區
教學專區
平面設計
語言：繁體中文
繁體中文
简体中文
English
熱門教材
熱門教材
開放式課程
熱門教材
高淑蓉
微積分一、二詳細版練習題
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
下載教材
Details
Course Name:
微積分一、二
Teacher:
高淑蓉
Time:
2015-06-12
Views:
11620
Social Share
捐贈愛心筆記
Tweet
Chapters
第1講 Syllabus, Limit and Continuity
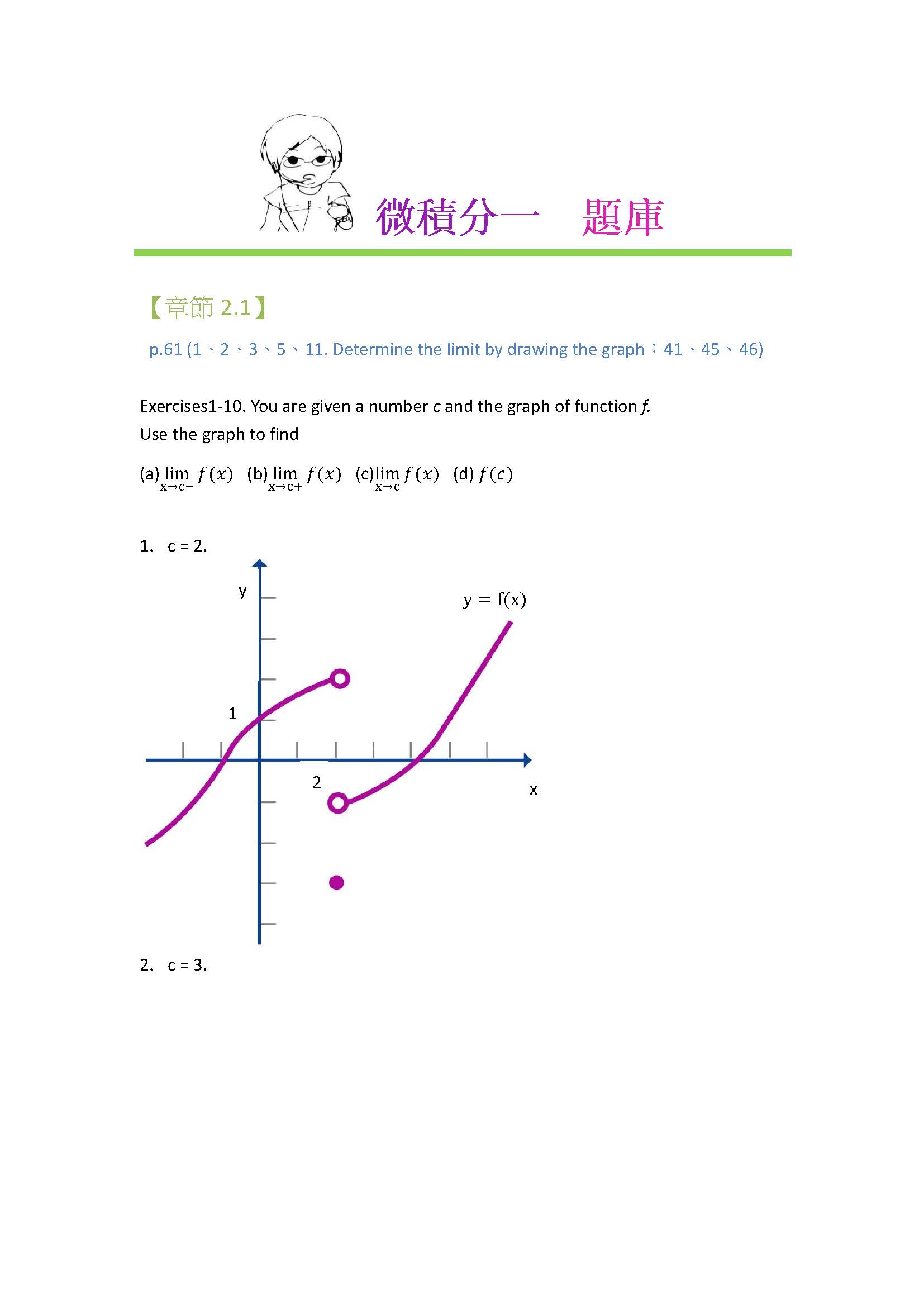
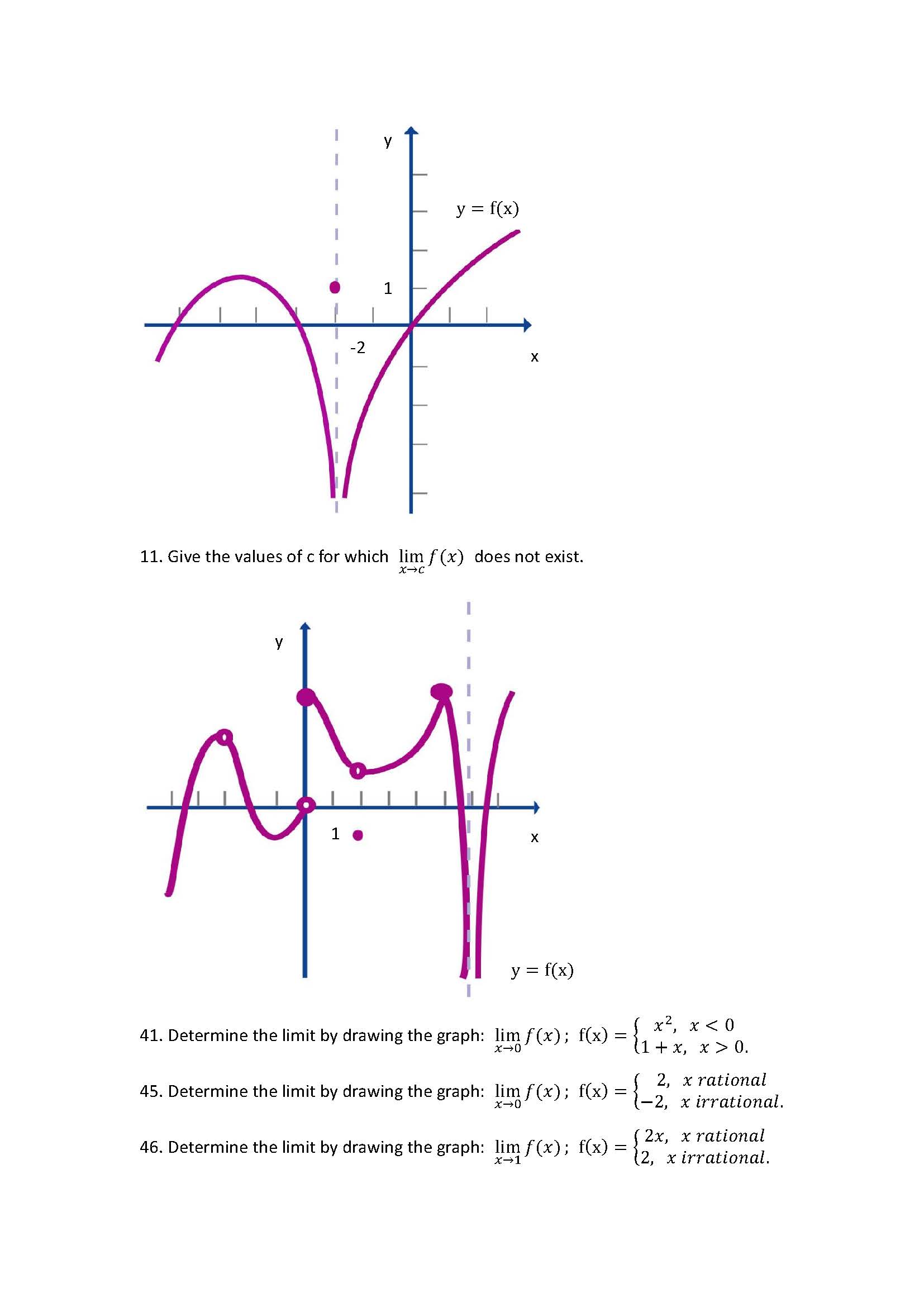
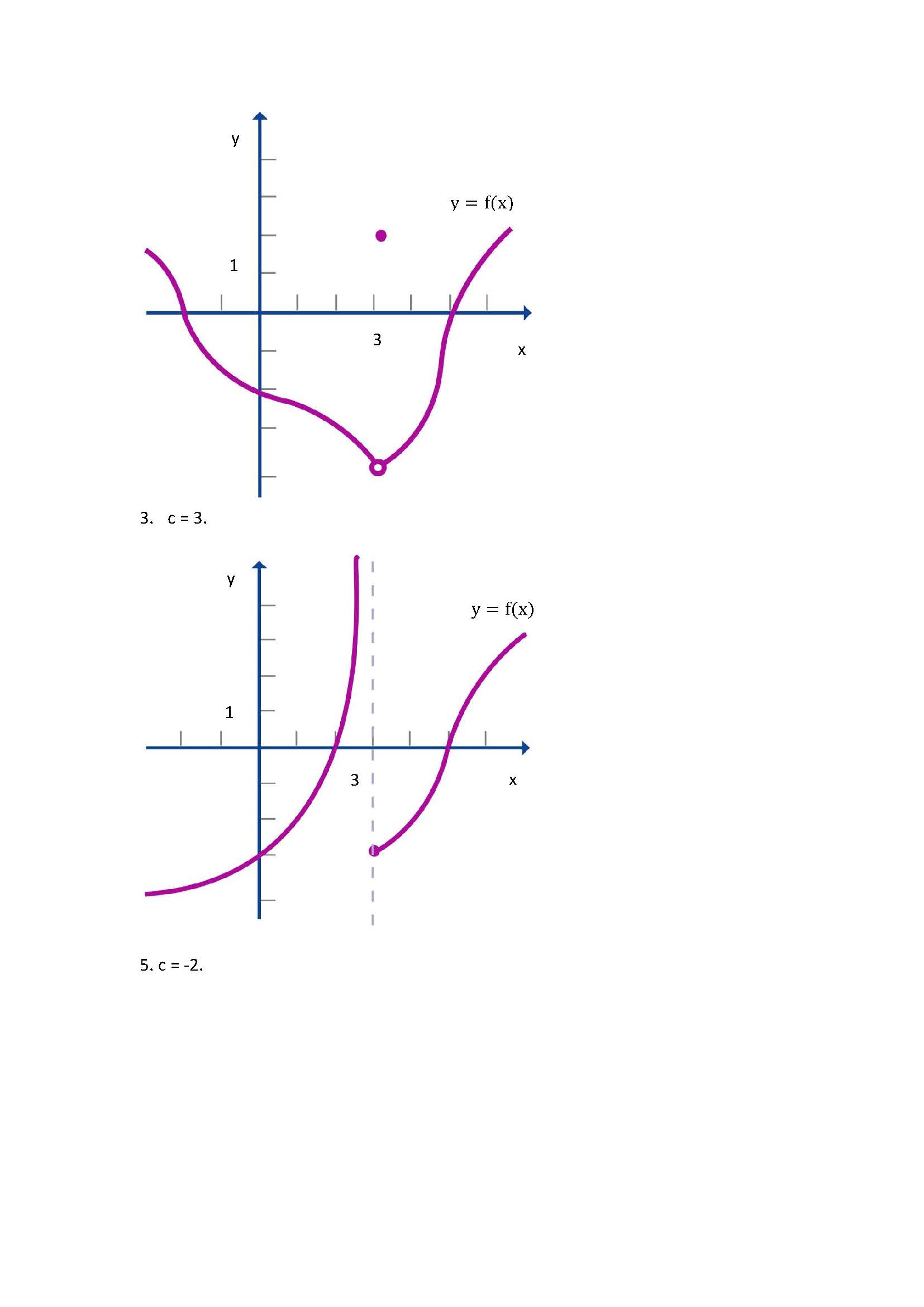
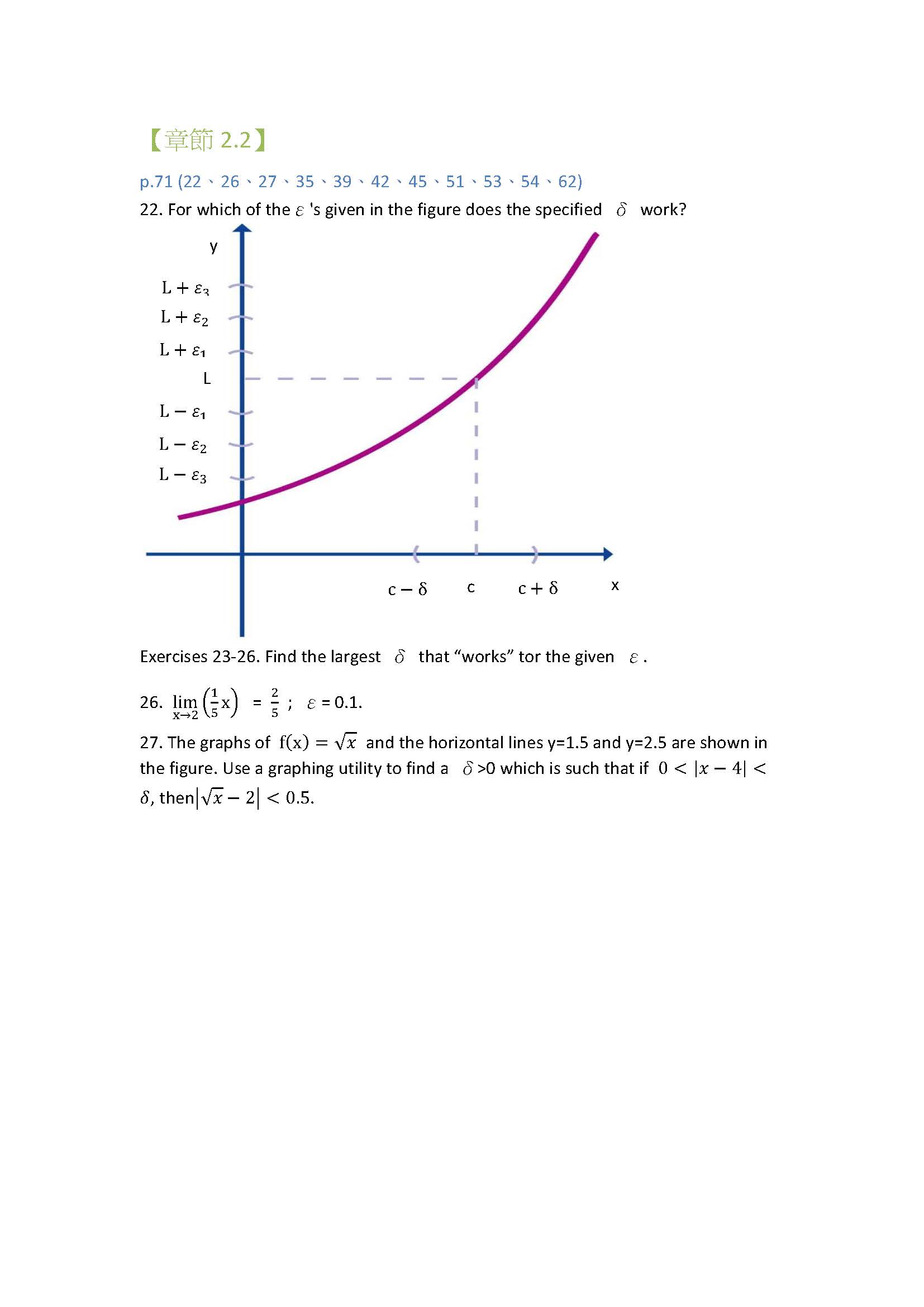
第2講 2.1, 2.2 極限、左極限和右極限
第3講 極限的數學建模
第4講 左右極限的數學建模 證明極限存在
第4講 左右極限的數學建模 證明極限存在
第5講 證明極限存在 極限的定理證明
第5講 證明極限存在 極限的定理證明
第5講 證明極限存在 極限的定理證明
第6講 2.3 Some Limit Theorems
第7講 極限的四則運算 極限的多項式
第8講 2.4 Continuity 證連續的四則運算 連續的合成函數
第8講 2.4 Continuity 證連續的四則運算 連續的合成函數
第9講 證明連續的合成函數、多項式 端點連續 2.5 夾擠定理 三角函數的連續
第10講 夾擠定理 三角函數的連續 2.6 中間值定理 極值定理
第11講 中間值定理的應用 3.1 derivate
第12講 可微分的性質 3.2 微分的四則運算 多項式的微分 3.3 微分的符號和高次項微分
第13講 3.4 視微分為變化率 3.5 連鎖律 3.6 三角函數微分 3.7隱函數微分...etc
第30講 續.三角函數的次數和乘積 8.4 三角替代法 8.5 部分分式
第30講 續.三角函數的次數和乘積 8.4 三角替代法 8.5 部分分式
第30講 續.三角函數的次數和乘積 8.4 三角替代法 8.5 部分分式
第14講 4.1 均值定理 端點的可微性 Thm A Rolle's thm
第15講 均值定理 4.2 遞增遞減函數
第16講 遞增遞減函數延拓到閉區間 微分相等的函數之間差一常數 4.3 局部極值
第17講 臨界點 一階二階導函數測試 圖形凹性和反曲點
第31講 續.部分分式 [Part 1] n維的座標系
第31講 續.部分分式 [Part 1] n維的座標系
第18講 利用圖形凹性和反曲點作圖 5.2 連續函數定積分 P的上和與下和
第19講 定義可積 廣義面積 連續必可積 黎曼和
第20講 5.3 面積函數 微積分第一基本定理
第21講 5.4 積分的均值定理 反導函數 微積分第二基本定理
第22講 續.微積分第二基本定理 5.7 變數變換
第23講 5.8 定積分額外性質 Ch.7 超越函數 §1 一對一函數和反函數
第24講 續.一對一函數和反函數
第25講 7.2 對數函數 part I
第26講 續.對數函數 part I, 7.3 對數函數 part II, 7.4 指數函數
第27講 續.指數函數 7.7 反三角函數
第28講 續.反三角函數 8.1 配方法 8.2 分部積分
第29講 8.3 三角函數的次數和乘積
第30講 續.三角函數的次數和乘積 8.4 三角替代法 8.5 部分分式
第30講 續.三角函數的次數和乘積 8.4 三角替代法 8.5 部分分式
第31講 續.部分分式 [Part 1] n維的座標系
第32講 續.[Part 1] n維的座標系 [Part 2] 向量
第33講 [Part 3] n維向量空間上的線和平面方程式 [Part 4] 集合的維度和函數的圖形
第1R講 Syllabus, Limit and Continuity
第2R講 2.1, 2.2 極限、左極限和右極限
第3R講 極限的數學建模
第4R講 左右極限的數學建模 證明極限存在 (check)
第5R講 證明極限存在 極限的定理證明(check)
第6R講 2.3 Some Limit Theorems(check)
第7R講 極限的四則運算 極限的多項式 (check)
第8R講 2.4 Continuity 證連續的四則運算 連續的合成函數 (check)
第9R講 證明連續的合成函數、多項式 端點連續 2.5 夾擠定理 三角函數的連續
第10R講 夾擠定理 三角函數的連續 2.6 中間值定理 極值定理
第11R講 中間值定理的應用 3.1 derivate
第12R講 可微分的性質 3.2 微分的四則運算 多項式的微分 3.3 微分的符號和高次項微分 (check)
第13R講 3.4 視微分為變化率 3.5 連鎖律 3.6 三角函數微分 3.7隱函數微分...etc
第14R講 4.1 均值定理 端點的可微性 Thm A Rolle's thm
第15R講 均值定理 4.2 遞增遞減函數
第16R講 遞增遞減函數延拓到閉區間 微分相等的函數之間差一常數 4.3 局部極值
第17R講 臨界點 一階二階導函數測試 圖形凹性和反曲點
第18R講 利用圖形凹性和反曲點作圖 5.2 連續函數定積分 P的上和與下和
第19R講 定義可積 廣義面積 連續必可積 黎曼和
第20R講 5.3 面積函數 微積分第一基本定理
第21R講 5.4 積分的均值定理 反導函數 微積分第二基本定理
第22R講 續.微積分第二基本定理 5.7 變數變換
第23R講 5.8 定積分額外性質 Ch.7 超越函數 §1 一對一函數和反函數
第24R講 續.一對一函數和反函數
第25R講 7.2 對數函數 part I
第26R講 續.對數函數 part I, 7.3 對數函數 part II, 7.4 指數函數 (check)
第27R講 續.指數函數 7.7 反三角函數
第28R講 續.反三角函數 8.1 配方法 8.2 分部積分 (check)
第29R講 8.3 三角函數的次數和乘積
第30R講 續.三角函數的次數和乘積 8.4 三角替代法 8.5 部分分式
第31R講 續.部分分式 [Part 1] n維的座標系
第32R講 續.[Part 1] n維的座標系 [Part 2] 向量
第33R講 [Part 3] n維向量空間上的線和平面方程式 [Part 4] 集合的維度和函數的圖形
第1講 續.[Part 4] 集合的維度和函數的圖形 向量函數
第2講 續.向量函數 向量函數的極限
第3講 續.向量函數的極限 向量函數的極限四則運算
第3講 續.向量函數的極限 向量函數的極限四則運算
第4講 向量函數的連續及連續的四則運算 向量函數的可微和可積及積分的四則運算
第5講 續.向量函數的可積四則運算 如何寫證明 14.2微分的基本法則 微分四則運算 14.3曲線
第6講 續.曲線 弧長
第7講 15.6 多變數函數的極限和連續
第8講 多變數函數的極限四則運算 多變數函數的連續 多變數函數的連續四則運算 多變數函數的合成
第9講 15.4 多變數函數的偏微分和混合微分
第10講 多變數函數偏微分的存在性無法保證其連續 二階偏微分的順序 16.1 可微分性 o(x)
第11講 o(x)的四則運算 單變數函數的可微 多變數的o(x) 多變數函數的可微 梯度
第12講 續.梯度 梯度的定理和性質
第14講 續.方向微分的定理 Gradients在工程上的意義 16.3 連鎖律
第15講 續.連鎖律 隱函數微分 Gradients在圖形上的意義
第16講 續.Gradients 在圖形上的意義 10.2 極座標
第17講 從極座標轉成直角座標 從直角坐標轉成極座標 10.3 Sketching curves in Polar Coordinates
第18講 極方程式的週期和作圖
第19講 心臟線、二瓣葉、漩渦 17.2 二變數函數積分 二變數函數在長方形上的積分
第20講 二變數函數的黎曼和 富比尼定理 重積分 二變數函數在一般區域上的積分 17.3 The evaluation of double integrals by repeated integral
第21講 17.3 The evaluation of double integrals by repeated integrals (Conti.) 17.4 極座標中的二變數函數積分
第22講 續.極座標中的二變數函數積分 15.2 二次曲面
第23講 續.二次曲面 17.6 Triple intrgrals 17.7 Reduced to repeated integrals
第24講 Reduced to repeated integrals (Conti.) 17.8 柱座標
第25講 續.柱座標 17.9 球面座標
第26講 Ch.11 數列和不定式 羅必達定理
第27講 數列的四則運算、合成函數和夾擠 等比數列的極限 單調數列 有上界或有下界或有界的數列 單調數列定理
第28講 12.2 無窮級數 等比級數 調和級數 級數的四則運算 12.3 積分與比較審歛法 p 級數, p 判別法
第29講 續.積分與比較審歛法 12.4 比值與根值判別法 12.5 絕對收斂和條件收斂;交替級數 交錯級數判別法
第30講 重組 12.6 泰勒多項式;泰勒數列 泰勒定理
第31講 Lagrange formula for remainder 泰勒數列 12.7 一般點上的泰勒多項式或數列
第32講 12.8 冪級數 冪級數的發散與收斂 收斂半徑 收斂區間 冪級數的微分性跟積分性
第33講 續.收斂半徑 Power Theorem 的微分定理 Term-by-term integration 積分跟微分有相同收斂半徑，但無相同收斂區間 在收斂區間內，冪級數就是本身和的泰勒級數
第1R講 續.[Part 4] 集合的維度和函數的圖形 向量函數
第2R講 續.向量函數 向量函數的極限
第5R講 續.向量函數的可積四則運算 如何寫證明 14.2微分的基本法則 微分四則運算 14.3曲線
第6R講 續.曲線 弧長
第7R講 15.6 多變數函數的極限和連續
第8R講 多變數函數的極限四則運算 多變數函數的連續 多變數函數的連續四則運算 多變數函數的合成
第9R講 15.4 多變數函數的偏微分和混合微分
第10R講 多變數函數偏微分的存在性無法保證其連續 二階偏微分的順序 16.1 可微分性 o(x)
第11R講 o(x)的四則運算 單變數函數的可微 多變數的o(x) 多變數函數的可微 梯度
第12R講 續.梯度 梯度的定理和性質
第14R講 續.方向微分的定理 Gradients在工程上的意義 16.3 連鎖律
第15R講 續.連鎖律 隱函數微分 Gradients在圖形上的意義
第16R講 續.Gradients 在圖形上的意義 10.2 極座標
第17R講 從極座標轉成直角座標 從直角坐標轉成極座標 10.3 Sketching curves in Polar Coordinates
第18R講 極方程式的週期和作圖
第19R講 心臟線、二瓣葉、漩渦 17.2 二變數函數積分 二變數函數在長方形上的積分
第20R講 二變數函數的黎曼和 富比尼定理 重積分 二變數函數在一般區域上的積分 17.3 The evaluation of double integrals by repeated integral
第21R講 17.3 The evaluation of double integrals by repeated integrals (Conti.) 17.4 極座標中的二變數函數積分
第22R講 續.極座標中的二變數函數積分 15.2 二次曲面
第23R講 續.二次曲面 17.6 Triple intrgrals 17.7 Reduced to repeated integrals
第24R講 Reduced to repeated integrals (Conti.) 17.8 柱座標
第25R講 續.柱座標 17.9 球面座標
第26R講 Ch.11 數列和不定式 羅必達定理
第27R講 數列的四則運算、合成函數和夾擠 等比數列的極限 單調數列 有上界或有下界或有界的數列 單調數列定理
第28R講 12.2 無窮級數 等比級數 調和級數 級數的四則運算 12.3 積分與比較審歛法 p 級數, p 判別法
第29R講 續.積分與比較審歛法 12.4 比值與根值判別法 12.5 絕對收斂和條件收斂;交替級數 交錯級數判別法
第30R講 重組 12.6 泰勒多項式;泰勒數列 泰勒定理
第31R講 Lagrange formula for remainder 泰勒數列 12.7 一般點上的泰勒多項式或數列
第32R講 12.8 冪級數 冪級數的發散與收斂 收斂半徑 收斂區間 冪級數的微分性跟積分性
第33R講 續.收斂半徑 Power Theorem 的微分定理 Term-by-term integration 積分跟微分有相同收斂半徑，但無相同收斂區間 在收斂區間內，冪級數就是本身和的泰勒級數
Categories
工程學群
自然科學學群
人文社會學群
專欄報導
學生筆記
